Quasisymmetry in Icosahedral Viruses

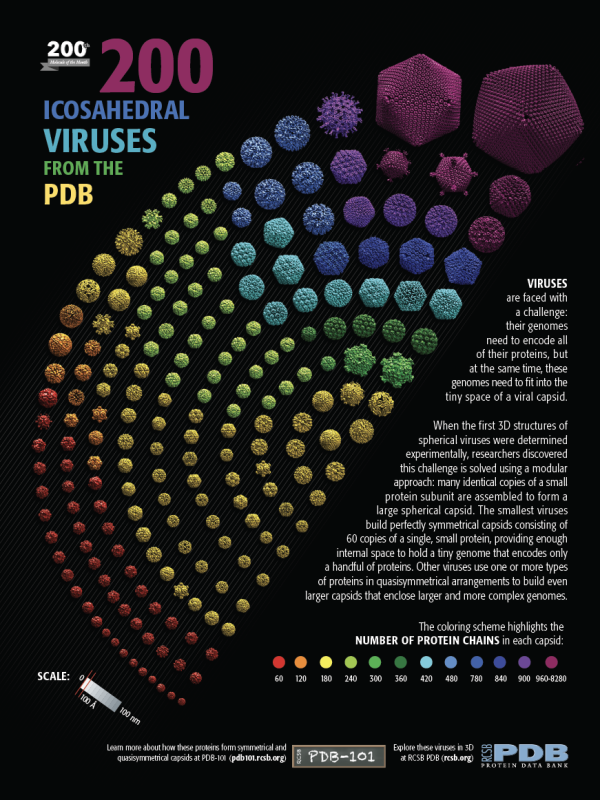
Viruses come in many shapes and sizes. Some of the simplest ones are composed of a spherical protein capsid that surrounds a strand of RNA or DNA that encodes the viral genome. The smallest examples have a capsid composed of 60 copies of a protein, arranged in icosahedral symmetry. Larger viruses have two options for building a larger capsid. They could build a much larger protein subunit, and assemble 60 of these in perfect icosahedral symmetry. This is rarely seen, however. Instead, larger viruses assemble capsids from many more copies of a single protein (or a few different proteins).

In the 1960’s, Donald Caspar and Aaron Klug discovered that viruses build these larger capsids by relaxing the need for perfect symmetry between the subunits. Small deformations in the way the subunits interact allow them to form pentagonal rings and hexagonal rings, which then assemble together to form larger “quasisymmetrical” capsids. They devised a way to classify these quasisymmetrical viruses based on a “triangulation number” that shows how many similar, but slightly different, conformations the subunits fit within the overall icosahedral symmetry.

Build 3D paper models of viruses with the templates below to explore the ways that quasisymmetry is used to build capsids with different sizes.

In a perfectly icosahedral virus, such as Satellite Tobacco Necrosis Virus, 60 protein subunits form pentagonal rings, which assemble into a shell with icosahedral symmetry. This is classified as T=1, since all subunits are in identical environments. Click on the image to download a template for two models: one based on the atomic structure (PDB entry 2buk) and one showing a schematic representation of the subunits.

A larger capsid with 180 subunits is built by Tomato Bushy Stunt Virus (TBSV) by using a subunit that can form pentagonal rings and hexagonal rings. The pentagons are arranged on the vertices of the icosahedron and the hexagons are arranged at the center of the faces. This capsid is assigned a triangulation number T=3, since the subunits need to adopt three slightly different quasisymmetrical conformations: one to build the pentagons and two to build the hexagons. Click on the image for a template to build a model of TBSV (PDB entry 2tbv) and a schematic model.

Nudaurelia capensis Omega Virus builds a larger capsid with 240 subunits with T=4 quasisymmetry. In this capsid, 60 subunits are arranged in pentagons at the vertices of the icosahedron, and the rest form hexamers centered on the edges of the icosahedron. Click on the image to build the atomic model (PDB entry 1ohf) and a schematic model.

Bacteriophage HK97 builds an even larger capsid with 420 subunits in T=7 quasisymmetry. As with the smaller viruses, 60 subunits form pentamers on the vertices, but three hexamers are then arranged on the faces.

Since this virus is much larger, the atomic model (PDB entry 1ohg) and the schematic model are included on separate pages.

Caspar and Klug discovered that we can explore some of the general principles of quasisymmetry by starting with a hexagonal network of subunits, as shown in blue in the background of all of these models. The trick is to trace out equilateral triangles on this network, and use them as the faces of an icosahedron. You can use this template to create quasisymmetrical viruses of larger triangulation numbers by discovering these larger triangles on the network. Triangles up to T=16 are shown to get you started.

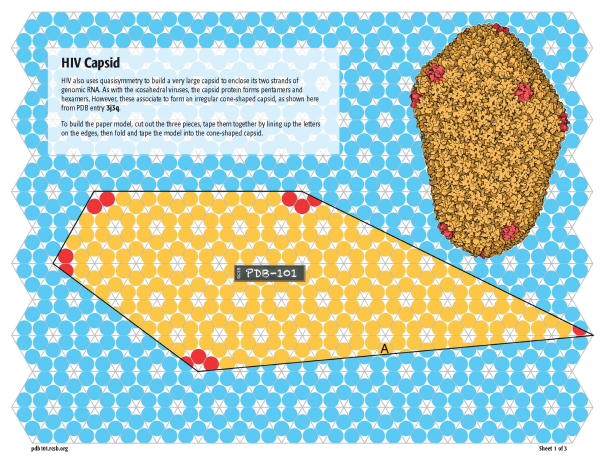
The capsid of HIV uses a similar approach, with many hexagons of subunits arranged between 12 pentagons of subunits (as seen in PDB entry 3j3q). But it doesn’t conform strictly to Caspar and Klug’s concept of quasisymmetry, resulting in an irregular cone-shaped capsid. You can build a model at the same scale as the icosahedral viruses using this schematic template on three pages.